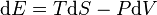The laws of thermodynamics

second law of thermodynamics, work can be totally converted into heat, but not vice versa. This is a mathematical consequence of statistical mechanics. The first law of thermodynamics simply asserts that energy is conserved,^[17] and that heat is included as a form of energy transfer. A commonly-used corollary of the first law is that for a "system" subject only to pressure forces and heat transfer (e.g., a cylinder-full of gas), the differential change in energy of the system (with a gain in energy signified by a positive quantity) is given as the following equation:

,

where the first term on the right is the heat transfer into the system, defined in terms of temperature T and entropy S (in which entropy increases and the change dS is positive when the system is heated), and the last term on the right hand side is identified as "work" done on the system, where pressure is P and volume V (the negative sign results since compression of the system requires work to be done on it and so the volume change, dV, is negative when work is done on the system). Although this equation is the standard textbook example of energy conservation in classical thermodynamics, it is highly specific, ignoring all chemical, electric, nuclear, and gravitational forces, effects such as advection of any form of energy other than heat, and because it contains a term that depends on temperature. The most general statement of the first law (i.e., conservation of energy) is valid even in situations in which temperature is undefinable.

Energy is sometimes expressed as the following equation:

,

which is unsatisfactory^[13] because there cannot exist any thermodynamic state functions W or Q that are meaningful on the right hand side of this equation, except perhaps in trivial cases.