What we now call gravity was not identified as a universal force until the work of Isaac Newton. Before Newton, the tendency for objects to fall towards the Earth was not understood to be related to the motions of celestial objects. Galileo was instrumental in describing the characteristics of falling objects by determining that the acceleration of every object in free-fall was constant and independent of the mass of the object. Today, this acceleration due to gravity towards the surface of the Earth is usually designated as 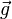 and has a magnitude of about 9.81 meters per second squared (this measurement is taken from sea level and may vary depending on location), and points toward the center of the Earth.[39] This observation means that the force of gravity on an object at the Earth's surface is directly proportional to the object's mass. Thus an object that has a mass of m will experience a force:
and has a magnitude of about 9.81 meters per second squared (this measurement is taken from sea level and may vary depending on location), and points toward the center of the Earth.[39] This observation means that the force of gravity on an object at the Earth's surface is directly proportional to the object's mass. Thus an object that has a mass of m will experience a force:
In free-fall, this force is unopposed and therefore the net force on the object is its weight. For objects not in free-fall, the force of gravity is opposed by the reactions of their supports. For example, a person standing on the ground experiences zero net force, since his weight is balanced by a normal force exerted by the ground.[3]
Newton's contribution to gravitational theory was to unify the motions of heavenly bodies, which Aristotle had assumed were in a natural state of constant motion, with falling motion observed on the Earth. He proposed a law of gravity that could account for the celestial motions that had been described earlier using Kepler's Laws of Planetary Motion.[40]
Newton came to realize that the effects of gravity might be observed in different ways at larger distances. In particular, Newton determined that the acceleration of the Moon around the Earth could be ascribed to the same force of gravity if the acceleration due to gravity decreased as an inverse square law. Further, Newton realized that the acceleration due to gravity is proportional to the mass of the attracting body.[40] Combining these ideas gives a formula that relates the mass (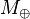 ) and the radius (
) and the radius ( ) of the Earth to the gravitational acceleration:
) of the Earth to the gravitational acceleration:
where the vector direction is given by 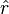 , the unit vector directed outward from the center of the Earth.[22]
, the unit vector directed outward from the center of the Earth.[22]
In this equation, a dimensional constant G is used to describe the relative strength of gravity. This constant has come to be known as Newton's Universal Gravitation Constant,[41] though its value was unknown in Newton's lifetime. Not until 1798 was Henry Cavendish able to make the first measurement of G using a torsion balance; this was widely reported in the press as a measurement of the mass of the Earth since knowing the G could allow one to solve for the Earth's mass given the above equation. Newton, however, realized that since all celestial bodies followed the same laws of motion, his law of gravity had to be universal. Succinctly stated, Newton's Law of Gravitation states that the force on a spherical object of mass m1 due to the gravitational pull of mass m2 is
where r is the distance between the two objects' centers of mass and 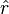 is the unit vector pointed in the direction away from the center of the first object toward the center of the second object.[22]
is the unit vector pointed in the direction away from the center of the first object toward the center of the second object.[22]
This formula was powerful enough to stand as the basis for all subsequent descriptions of motion within the solar system until the twentieth century. During that time, sophisticated methods of perturbation analysis[42] were invented to calculate the deviations of orbits due to the influence of multiple bodies on a planet, moon, comet, or asteroid. The formalism was exact enough to allow mathematicians to predict the existence of the planet Neptune before it was observed.[43]
It was only the orbit of the planet Mercury that Newton's Law of Gravitation seemed not to fully explain. Some astrophysicists predicted the existence of another planet (Vulcan) that would explain the discrepancies; however, despite some early indications, no such planet could be found. When Albert Einstein finally formulated his theory of general relativity (GR) he turned his attention to the problem of Mercury's orbit and found that his theory added a correction which could account for the discrepancy. This was the first time that Newton's Theory of Gravity had been shown to be less correct than an alternative.[44]
Since then, and so far, general relativity has been acknowledged as the theory which best explains gravity. In GR, gravitation is not viewed as a force, but rather, objects moving freely in gravitational fields travel under their own inertia in straight lines through curved space-time –


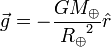
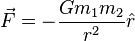


0 comments:
Post a Comment