Forces can be used to define a number of physical concepts by integrating with respect to kinematic variables. For example, integrating with respect to time gives the definition of impulse[61]
which, by Newton's Second Law, must be equivalent to the change in momentum (yielding the Impulse momentum theorem).
Similarly, integrating with respect to position gives a definition for the work done by a force:[62]
which is equivalent to changes in kinetic energy (yielding the work energy theorem).[62]
Power P is the rate of change dW/dt of the work W, as the trajectory is extended by a position change 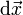 in a time interval dt:[63]
in a time interval dt:[63]
with 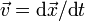 the velocity.
the velocity.
[edit] Potential energy
Instead of a force, often the mathematically related concept of a potential energy field can be used for convenience. For instance, the gravitational force acting upon an object can be seen as the action of the gravitational field that is present at the object's location. Restating mathematically the definition of energy (via the definition of work), a potential scalar field  is defined as that field whose gradient is equal and opposite to the force produced at every point:
is defined as that field whose gradient is equal and opposite to the force produced at every point:
Forces can be classified as conservative or nonconservative. Conservative forces are equivalent to the gradient of a potential while non-conservative forces are not.[3]

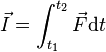
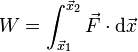
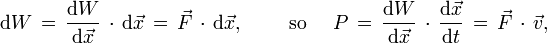
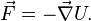


0 comments:
Post a Comment