Rotations and torque

Forces that cause extended objects to rotate are associated with torques. Mathematically, the torque on a particle is defined as the cross-product:

where

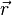is the particle's position vector relative to a pivot

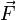is the force acting on the particle.

Torque is the rotation equivalent of force in the same way that angle is the rotational equivalent for position, angular velocity for velocity, and angular momentum for momentum. All the formal treatments of Newton's Laws that applied to forces equivalently apply to torques. Thus, as a consequence of Newton's First Law of Motion, there exists rotational inertia that ensures that all bodies maintain their angular momentum unless acted upon by an unbalanced torque. Likewise, Newton's Second Law of Motion can be used to derive an alternative definition of torque:

where

I is the moment of inertia of the particle

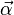is the angular acceleration of the particle.

This provides a definition for the moment of inertia which is the rotational equivalent for mass. In more advanced treatments of mechanics, the moment of inertia acts as a tensor that, when properly analyzed, fully determines the characteristics of rotations including precession and nutation.

Equivalently, the differential form of Newton's Second Law provides an alternative definition of torque:

^[58]

where is the angular momentum of the particle.

Newton's Third Law of Motion requires that all objects exerting torques themselves experience equal and opposite torques,^[59] and therefore also directly implies the conservation of angular

Relationship between force (F), torque (τ), and momentum vectors (p and L) in a rotating system.

momentum for closed systems that experience rotations and revolutions through the action of internal torques.