In microcanonical ensemble N, V and E are fixed. Since the second law of thermodynamics applies to isolated systems, the first case investigated will correspond to this case. The Microcanonical ensemble describes an isolated system.
The entropy of such a system can only increase, so that the maximum of its entropy corresponds to an equilibrium state for the system.
Because an isolated system keeps a constant energy, the total energy of the system does not fluctuate. Thus, the system can access only those of its micro-states that correspond to a given value E of the energy. The internal energy of the system is then strictly equal to its energy.
Let us call Ω(E) the number of micro-states corresponding to this value of the system's energy. The macroscopic state of maximal entropy for the system is the one in which all micro-states are equally likely to occur, with probability 1 / Ω(E), during the system's fluctuations.
-
- where
- S is the system entropy, and
- kB is Boltzmann's constant.

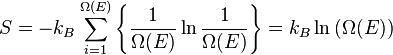


0 comments:
Post a Comment