Posts
Because energy is strictly conserved and is also locally conserved (wherever it can be defined), it is important to remember that by the definition of energy the transfer of energy between the "system" and adjacent regions is work. A familiar example is mechanical work. In simple cases this is written as the following equation:
- ΔE = W (1)
if there are no other energy-transfer processes involved. Here E is the amount of energy transferred, and W represents the work done on the system.
More generally, the energy transfer can be split into two categories:
- ΔE = W + Q (2)
where Q represents the heat flow into the system.
There are other ways in which an open system can gain or lose energy. In chemical systems, energy can be added to a system by means of adding substances with different chemical potentials, which potentials are then extracted (both of these process are illustrated by fueling an auto, a system which gains in energy thereby, without addition of either work or heat). Winding a clock would be adding energy to a mechanical system. These terms may be added to the above equation, or they can generally be subsumed into a quantity called "energy addition term E" which refers to any type of energy carried over the surface of a control volume or system volume. Examples may be seen above, and many others can be imagined (for example, the kinetic energy of a stream of particles entering a system, or energy from a laser beam adds to system energy, without either being either work-done or heat-added, in the classic senses).
- ΔE = W + Q + E (3)
Where E in this general equation represents other additional advected energy terms not covered by work done on a system, or heat added to it.
Energy is also transferred from potential energy (Ep) to kinetic energy (Ek) and then back to potential energy constantly. This is referred to as conservation of energy. In this closed system, energy cannot be created or destroyed; therefore, the initial energy and the final energy will be equal to each other. This can be demonstrated by the following:
- Epi + Eki = EpF + EkF
The equation can then be simplified further since Ep = mgh (mass times acceleration due to gravity times the height) and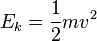 
(half mass times velocity squared). Then the total amount of energy can be found by adding Ep + Ek = Etotal.
Energy and the laws of motion
| Classical mechanics | ||||||
 Newton's Second Law | ||||||
History of ...
| ||||||
In classical mechanics, energy is a conceptually and mathematically useful property, as it is a conserved quantity.
The Hamiltonian
The total energy of a system is sometimes called the Hamiltonian, after William Rowan Hamilton. The classical equations of motion can be written in terms of the Hamiltonian, even for highly complex or abstract systems. These classical equations have remarkably direct analogs in nonrelativistic quantum mechanics.[15]
0 comments:
Post a Comment