Mechanical energy manifest in many forms,but can be broadly classified into elastic potential energy and kinetic energy. The term potential energy is a very general term, because it exists in all force fields, such as gravitation, electrostatic and magnetic fields. Potential energy refers to the energy any object gets due to its position in a force field.
Potential energy, symbols Ep, V or Φ, is defined as the work done against a given force (= work of given force with minus sign) in changing the position of an object with respect to a reference position (often taken to be infinite separation). If F is the force and s is the displacement,
with the dot representing the scalar product of the two vectors.
The name "potential" energy originally signified the idea that the energy could readily be transferred as work—at least in an idealized system (reversible process, see below). This is not completely true for any real system, but is often a reasonable first approximation in classical mechanics.
The general equation above can be simplified in a number of common cases, notably when dealing with gravity or with elastic forces.
Elastic potential energy

Elastic potential energy is defined as a work needed to compress (or expand) a spring. The force, F, in a spring or any other system which obeys Hooke's law is proportional to the extension or compression, x,
-
- F = − kx
where k is the force constant of the particular spring (or system). In this case, the calculated work becomes
only when k is constant. Hooke's law is a good approximation for behaviour of chemical bonds under normal conditions, i.e. when they are not being broken or formed.
Kinetic energy
Kinetic energy, symbols Ek, T or K, is the work required to accelerate an object to a given speed. Indeed, calculating this work one easily obtains the following:
At speeds approaching the speed of light, c, this work must be calculated using Lorentz transformations, which results in the following:
This equation reduces to the one above it, at small (compared to c) speed. A mathematical by-product of this work (which is immediately seen in the last equation) is that even at rest a mass has the amount of energy equal to:
-
- Erest = mc2
This energy is thus called rest mass energy.

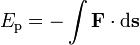

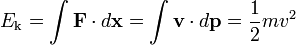



0 comments:
Post a Comment