For a simple compressible system such as an ideal gas inside a piston, the changes in enthalpy and internal energy can be related to the heat capacity at constant pressure and volume, respectively. Constrained to have constant volume, the heat, Q, required to change its temperature from an initial temperature, T0, to a final temperature, Tf is given by:
Removing the volume constraint and allowing the system to expand or contract at constant pressure:
For incompressible substances, such as solids and liquids, the distinction between the two types of heat capacity disappears, as no work is performed. Heat capacity is an extensive quantity and as such is dependent on the number of molecules in the system. It can be represented as the product of mass, m , and specific heat capacity,  according to:
according to:
or is dependent on the number of moles and the molar heat capacity,  according to:
according to:
The molar and specific heat capacities are dependent upon the internal degrees of freedom of the system and not on any external properties such as volume and number of molecules.
The specific heats of monatomic gases (e.g., helium) are nearly constant with temperature. Diatomic gases such as hydrogen display some temperature dependence, and triatomic gases (e.g., carbon dioxide) still more.
In liquids at sufficiently low temperatures, quantum effects become significant. An example is the behavior of bosons such as helium-4. For such substances, the behavior of heat capacity with temperature is discontinuous at the Bose-Einstein condensation point.
The quantum behavior of solids is adequately characterized by the Debye model. At temperatures well below the characteristic Debye temperature of a solid lattice, its specific heat will be proportional to the cube of absolute temperature. For low-temperature metals, a second term is needed to account for the behavior of the conduction electrons, an example of Fermi-Dirac statistics.
[edit] Phase Changes
The boiling point of water, at sea level and normal atmospheric pressure and temperature, will always be at nearly 100 °C, no matter how much heat is added. The extra heat changes the phase of the water from liquid into water vapor. The heat added to change the phase of a substance in this way is said to be "hidden" and thus it is called latent heat (from the Latin latere meaning "to lie hidden"). Latent heat is the heat per unit mass necessary to change the state of a given substance, or:
and
Note that, as pressure increases, the L rises slightly. Here, Mo is the amount of mass initially in the new phase, and M is the amount of mass that ends up in the new phase. Also, L generally does not depend on the amount of mass that changes phase, so the equation can normally be written:
- Q = LΔm.
Sometimes L can be time-dependent if pressure and volume are changing with time, so that the integral can be written as:
heat only travels one way

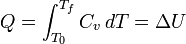
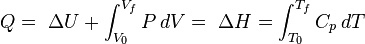


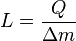
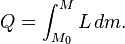
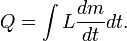


0 comments:
Post a Comment