Force and displacement are both vector quantities and they are combined using the dot product to evaluate the mechanical work, a scalar quantity:
 (1)
(1)
where  is the angle between the force and the displacement vector.
is the angle between the force and the displacement vector.
In order for this formula to be valid, the force and angle must remain constant. The object's path must always remain on a single, straight line, though it may change directions while moving along the line.
In situations where the force changes over time, or the path deviates from a straight line, equation (1) is not generally applicable although it is possible to divide the motion into small steps, such that the force and motion are well approximated as being constant for each step, and then to express the overall work as the sum over these steps.
The general definition of mechanical work is given by the following line integral:
 (2)
(2)
where:
 is the path or curve traversed by the object;
is the path or curve traversed by the object;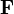 is the force vector; and
is the force vector; and is the position vector.
is the position vector.
The expression  is an inexact differential which means that the calculation of
is an inexact differential which means that the calculation of  is path-dependent and cannot be differentiated to give
is path-dependent and cannot be differentiated to give  .
.
Equation (2) explains how a non-zero force can do zero work. The simplest case is where the force is always perpendicular to the direction of motion, making the integrand always zero. This is what happens during circular motion. However, even if the integrand sometimes takes nonzero values, it can still integrate to zero if it is sometimes negative and sometimes positive.
The possibility of a nonzero force doing zero work illustrates the difference between work and a related quantity, impulse, which is the integral of force over time. Impulse measures change in a body's momentum, a vector quantity sensitive to direction, whereas work considers only the magnitude of the velocity. For instance, as an object in uniform circular motion traverses half of a revolution, its centripetal force does no work, but it transfers a nonzero impulse.
[edit] Torque and rotation
Work done by a torque can be calculated in a similar manner. A torque  applied through a revolution of
applied through a revolution of 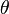 , expressed in radians, does work as follows:
, expressed in radians, does work as follows:

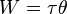


0 comments:
Post a Comment