The first law of thermodynamics, an expression of the principle of conservation of energy, states that energy can be transformed (changed from one form to another), but cannot be created or destroyed.
| “ | The increase in the internal energy of a system is equal to the amount of energy added by heating the system minus the amount lost as a result of the work done by the system on its surroundingsDescriptionThe first law of thermodynamics says that energy is conserved in any process involving a thermodynamic system and its surroundings. Frequently it is convenient to focus on changes in the assumed internal energy (U) and to regard them as due to a combination of heat (Q) added to the system and work done by the system (W). Taking dU as an incremental (differential) change in internal energy, one writes where δQ and δW are incremental changes in heat and work, respectively. Note that the minus sign in front of δW indicates that a positive amount of work done by the system leads to energy being lost from the system. Depending on discipline, an alternative convention may be adopted for the "work" under consideration, leading to: where
Work and heat are due to processes which add or subtract energy, while U is a particular form of energy associated with the system. Thus the term "heat energy" for δQ means "that amount of energy added as the result of heating" rather than referring to a particular form of energy. Likewise, "work energy" for δw means "that amount of energy lost as the result of work". Internal energy is a property of the system whereas work done and heat supplied are not. A significant result of this distinction is that a given internal energy change (dU) can be achieved by, in principle, many combinations of heat and work. Informally, the law was first formulated by Germain Hess via Hess's Law, and later by Julius Robert von Mayer[2] The first explicit statement of the first law of thermodynamics was given by Rudolf Clausius in 1850: "There is a state function E, called ‘energy’, whose differential equals the work exchanged with the surroundings during an adiabatic process." Mathematical formulationThe infinitesimal heat and work in the equations above are denoted by δ rather than d because, in mathematical terms, they are not exact differentials. In other words, they do not describe the state of any system. The integral of an inexact differential depends upon the particular "path" taken through the space of thermodynamic parameters while the integral of an exact differential depends only upon the initial and final states. If the initial and final states are the same, then the integral of an inexact differential may or may not be zero, but the integral of an exact differential will always be zero. The path taken by a thermodynamic system through a chemical or physical change is known as a thermodynamic process. An expression of the first law can be written in terms of exact differentials by realizing that the work that a system does is, in case of a reversible process, equal to its pressure times the infinitesimal change in its volume. In other words δw = PdV where P is pressure and V is volume. Also, for a reversible process, the total amount of heat added to a system can be expressed as δQ = TdS where T is temperature and S is entropy. Therefore, for a reversible process: Since U, S and V are thermodynamic functions of state, the above relation holds also for non-reversible changes. The above equation is known as the fundamental thermodynamic relation. In the case where the number of particles in the system is not necessarily constant and may be of different types, the first law is written: where dNi is the (small) number of type-i particles added to the system, and μi is the amount of energy added to the system when one type-i particle is added, where the energy of that particle is such that the volume and entropy of the system remains unchanged. μi is known as the chemical potential of the type-i particles in the system. The statement of the first law, using exact differentials is now: If the system has more external variables than just the volume that can change, the fundamental thermodynamic relation generalizes to: Here the Xi are the generalized forces corresponding to the external variables xi. A useful idea from mechanics is that the energy gained by a particle is equal to the force applied to the particle multiplied by the displacement of the particle while that force is applied. Now consider the first law without the heating term: dU = − PdV. The pressure P can be viewed as a force (and in fact has units of force per unit area) while dV is the displacement (with units of distance times area). We may say, with respect to this work term, that a pressure difference forces a transfer of volume, and that the product of the two (work) is the amount of energy transferred as a result of the process. It is useful to view the TdS term in the same light: With respect to this heat term, a temperature difference forces a transfer of entropy, and the product of the two (heat) is the amount of energy transferred as a result of the process. Here, the temperature is known as a "generalized" force (rather than an actual mechanical force) and the entropy is a generalized displacement. Similarly, a difference in chemical potential between groups of particles in the system forces a transfer of particles, and the corresponding product is the amount of energy transferred as a result of the process. For example, consider a system consisting of two phases: liquid water and water vapor. There is a generalized "force" of evaporation which drives water molecules out of the liquid. There is a generalized "force" of condensation which drives vapor molecules out of the vapor. Only when these two "forces" (or chemical potentials) are equal will there be equilibrium, and the net transfer will be zero. The two thermodynamic parameters which form a generalized force-displacement pair are termed "conjugate variables". The two most familiar pairs are, of course, pressure-volume, and temperature-entropy. Types of thermodynamic processesPaths through the space of thermodynamic variables are often specified by holding certain thermodynamic variables constant. It is useful to group these processes into pairs, in which each variable held constant is one member of a conjugate pair. The pressure-volume conjugate pair is concerned with the transfer of mechanical or dynamic energy as the result of work.
The temperature-entropy conjugate pair is concerned with the transfer of thermal energy as the result of heating.
The above have all implicitly assumed that the boundaries are also impermeable to particles. We may assume boundaries that are both rigid and thermally insulating, but are permeable to one or more types of particle. Similar considerations then hold for the (chemical potential)-(particle number) conjugate pairs. |

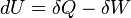
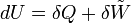
 is the work done on the system by the surroundings.
is the work done on the system by the surroundings.






0 comments:
Post a Comment